Answer:
9x⁶y⁴
Step-by-step explanation:
The area of a rectangle is equal to:
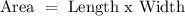
So, dividend both sides by the length, we get that the width can be calculated as:
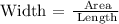
Then, replacing the expression for the Area and the length, we get:
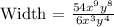
Now, we will use the following property:
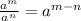
It means that when we divide two numbers with the same base, we subtract the exponents. So, the width is equal to:
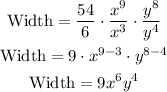
Therefore, the expression that represents the width of the rectangle in yards is: 9x⁶y⁴