Question

Need help with homework

Answer 1

We have two points describing the diameter of a circumference, these are:

`\begin{gathered} A=(-12,-4) \\ B=(-4,-10) \end{gathered}`

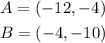
Recall that the equation for the standard form of a circle is:

`(x-h)^2+(y-k)^2=r^2`

Where (h,k) is the coordinate of the center of the circle, to find this coordinate, we find the midpoint of the diameter, that is, the midpoint between points A and B.

For this we use the following equation:

`M=(\frac{x_1+x_2_{}_{}}{2},(y_1+y_2)/(2))`

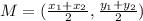
Now, we replace and solve:

`\begin{gathered} M=((-12+(-4))/(2),(-4+(-10))/(2) \\ M=((-12-4)/(2),(-4-10)/(2)) \\ M=((-16)/(2),(-14)/(2)) \\ M=(-8,-7) \end{gathered}`

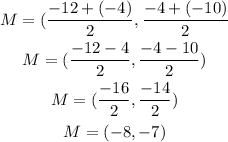
The center of the circle is (-8,-7), so:

`\begin{gathered} h=-8 \\ k=-7 \end{gathered}`

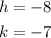
On the other hand, we must find the radius of the circle, remember that the radius of a circle goes from the center of the circumference to a point on its arc, for this we use the following equation:

`r^2=\Delta x^2+\Delta y^2`

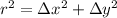
In this case, we will solve the delta with the center coordinate and the B coordinate.

`\begin{gathered} r^2=((-4)-(-8))^2+((-10)-(-7)) \\ r^2=(-4+8)^2+(-10+7)^2 \\ r^2=4^2+(-3)^2 \\ r^2=16+9 \\ r^2=25 \\ r=5 \end{gathered}`

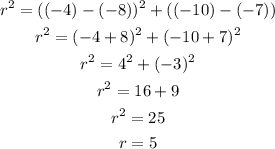
Therefore, the equation for the standard form of a circle is:

`\begin{gathered} (x-(-8))^2+(y-(-7))^2=25 \\ (x+8)^2+(y+7)^2=25 \end{gathered}`

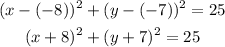
In conclusion, the equation is the following:

`(x+8)^2+(y+7)^2=25`