1 Answer

Daniel Myers · Answer 1 · 2023-12-25T02:46:12+0000

ANSWER

85.9° North of East

Step-by-step explanation

First, we have to make a sketch:

We have to find the resultant vector of the car's displacement.

The horizontal component of the displacement of the car:

$\begin{gathered} d_x=-10\cos 45+15\cos 60 \\ d_x=(-10\cdot0.7071)+(15\cdot0.5)=-7.071+7.5 \\ d_x=0.429\operatorname{km} \end{gathered}$

The vertical component of the displacement of the car is:

$\begin{gathered} d_y=-10\sin 45+15\sin 60 \\ d_y=(-10\cdot0.7071)+_{}(15\cdot0.8660)=-7.071+12.990 \\ d_y=5.919\operatorname{km} \end{gathered}$

To find the direction of the car's resultant vector, apply the formula:

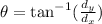
$\theta=\tan ^(-1)((d_y)/(d_x))$

Therefore, we have:

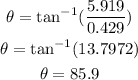
$\begin{gathered} \theta=\tan ^(-1)((5.919)/(0.429)) \\ \theta=\tan ^(-1)(13.7972) \\ \theta=85.9\degree \end{gathered}$

Hence, the car's resultant vector is 85.9° North of East.

Your comment on this question: