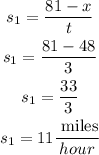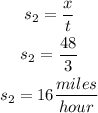Speed (s) is defined as follows:
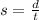
where d is distance and t is time.
Let's call x to the distance traveled by one of the cyclists. Combining the distance traveled by both cyclists, they rode 81 miles. Then, if one cyclist rode x miles, then the other one traveled (81 - x) miles, that is,

Where d1 and d2 are the distances traveled.
Substituting into the speed formula:
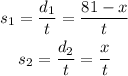
They traveled 3 hours, then t = 3 in both equations.
We also know that one cyclist travels 5 miles/h slower than the other one. Therefore:

Solving for x:
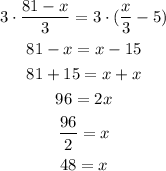
Substituting this result into the speed equations: