Question

Find the values of where the tangent line to the graph of f(x) = 1/x is parallel to the line y = - 7x + 8

Answer 1

Given:

`y=-7x+8`

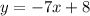
Let's find the values of x where the tangent line to the graph of f(x) is parallel to the given line.

Where:

`f(x)=(1)/(x)`

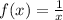
Let's first find the derivative of f(x).

We have:

`\begin{gathered} f^(\prime)(x)=(d)/(dx)((1)/(x)) \\ \\ f^(\prime)(x)=(1)/(x^2) \end{gathered}`

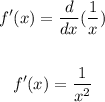
Apply the slope-intercept form:

y = mx + b

Where m is the slope.

Now, from the equation:

y = -7x + 8

The slope of the line is -7.

Now if the tangent of f(x) =1/x is parallel to the line, f'(x) will be the slope of the line.

Thus, we have:

`-(1)/(x^2)=-7`

Now, let's solve for the values of x.

Multiply both sides by x²:

`\begin{gathered} -(1)/(x^2)*x^2=-7x^2 \\ \\ -1=-7x^2 \end{gathered}`

Divide both sides by -7:

`\begin{gathered} (-1)/(-7)=-(7x^2)/(-7) \\ \\ (1)/(7)=x^2 \\ \\ x^2=(1)/(7) \end{gathered}`

Take the square root of both sides:

`\begin{gathered} √(x^2)=\pm\sqrt{(1)/(7)} \\ \\ x=\pm(√(1))/(√(7)) \end{gathered}`

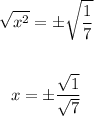
Solving further:

`\begin{gathered} x=\pm(1)/(√(7)) \\ \\ x=-(1)/(√(7)),(1)/(√(7)) \end{gathered}`

Therefore, we have the following:

• The greater solution is x = 1/sqrt(7)

,

• The lesser solution is x = -1/sqrt(7).

ANSWER:

• The greater solution is x = 1/sqrt(7)

,

• The lesser solution is x = -1/sqrt(7).