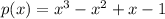Question

Build a polynomial of degree 3 with real coefficients and zeros 1 and I

Answer 1

Polynomials

A polynomial can be built if we know its zeros, also called roots

Suppose p,q, and r are the roots of a polynomial of degree 3, then:

p(x)=a(x-p)(x-q)(x-r)

Where a is a real number different from 0

Note we are only given two roots:

p=1

q=i

recall that i is the base of the complex numbers, that is:

`\mathbf{i}=√(-1)`

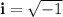
The third root comes when we recall that, if a polynomial has real coefficients, the complex roots come in conjugate pairs, i.e. if a+bi is one root of the polynomial, then a-bi is also a root of the polynomial.

Thus, the other root is the conjugate of q:

r=-i

Now we have all the roots, we just apply the above equation to find:

p(x)=a(x-p)(x-q)(x-r)

p(x)=a(x-1)(x-i)(x+i)

Recall that

`\mleft(x-i\mright)\mleft(x+i\mright)=x^2-i^2`

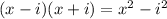
Since

`i^2=-1`
`(x-i)(x+i)=x^2+1`

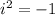
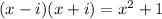
Finally, the required polynomial is:

`p\mleft(x\mright)=a\mleft(x-1\mright)(x^2+1)`

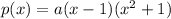
Since no other condition is given, we choose a=1:

`p(x)=(x-1)(x^2+1)`

This is the required polynomial

Operating the products:

`p(x)=(x-1)(x^2+1)=x^3+x-x^2-1`

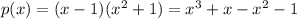
Ordering:

`p(x)=x^3-x^2+x-1`