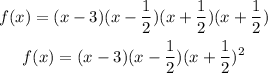The given polynomial is:
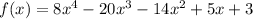
b. Use the synthetic division to show 3 is a zero of f(x):
To apply synthetic division, start listing all the coefficients of the polynomial in order (descending powers). If there are any missing terms you write a 0.
The divisor goes out of the box (the zero you want to evaluate :3).
After that, bring down the leading coefficient to the bottom row (8).
Multiply the divisor by the value just written on the bottom row, and write the result right beneath the next coefficient in the dividend (3x8=24).
Add the two values in column 3 and write the result in the bottom row (-20+24=4).
Follow the same procedure until the end.
The numbers in the last row make up your coefficients of the quotient as well as the remainder (this is the final value on the right). Working right to left, the next number is your constant, the next is the coefficient for x, the next is the coefficient for x^2, etc.
As the remainder is 0, then 3 is a zero of f(x):

c. Find the remaining zeros of f(x):
Let's use synthetic division as well to evaluate if 1/2 is a zero of f(x): 1/2=0.5, then:
As the remainder is 0, 1/2 is a zero of f(x):

Now, let's evaluate -1/2=-0.5 by using synthetic division:
As the remainder is 0, -1/2 is a zero of f(x) too:
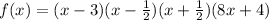
d.Write the complete linear factorization of f(x):
You can write 8x+4 as x+1/2 by dividing both terms by 8, then: