Question

Find the probability of selecting a red card or a 4 from a deck of 52 cards.A.7/13B.15/26C.6/13D.3/5

Answer 1

The probabilityIna deck of 52 cards, there are 26 red cards and 4 cards numbered 4.

Thus,

`\begin{gathered} \text{Number of red cards = n(red cards) =26} \\ \text{Number of 4 = n(4) = 4} \\ \text{Total number of cards in a deck = 52} \end{gathered}`

Probability of an event is evaluated as

`Pr\text{ = }\frac{\text{number of favourable outcomes}}{\text{total number of possible outcomes}}`

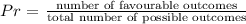
Thus,

`\begin{gathered} \text{Probability of picking a red card = Pr(R)=}\frac{\text{number of red cards}}{total\text{ number of cards}} \\ Pr(R\text{) = }\frac{\text{26}}{52}=(1)/(2) \\ \Rightarrow Pr(R\text{) = }(1)/(2) \end{gathered}`

Similarly,

`\begin{gathered} \text{Probability of picking a 4 = Pr(4) = }\frac{\text{total number of 4}}{total\text{ number of cards}} \\ Pr(4)=(4)/(52)\text{ = }(1)/(13) \\ \Rightarrow Pr(4_{_{}})=\text{ }(1)/(13) \end{gathered}`

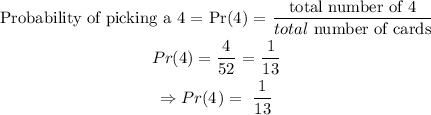
The probability of selecting a red card or a 4 is evaluated as

`\begin{gathered} Pr(R\text{ }\cup\text{ 4) = Pr(R) + Pr(4) } \\ =\text{ }(1)/(2)\text{ + }(1)/(13) \\ \text{LCM = 26} \\ \Rightarrow(13+2)/(26)\text{ =}(15)/(26) \\ Pr(R\text{ }\cup\text{ 4)=}(15)/(26) \end{gathered}`

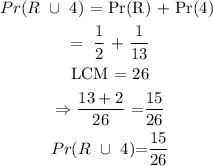
Thus, the probability of selecting a red card or a 4 from a deck of 52 cards is

`(15)/(26)`

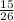
The correct option is B