Question

This is a practice problem I made up and would love some help with solving.Not from an assignment :)

Answer 1

Step-by-step explanation:

Given:

`\begin{gathered} x(\theta)=3\cos\theta \\ y(\theta)=2\sin\theta \\ where\text{ }\theta\text{ lies between }(\pi)/(2)\text{ and }(3\pi)/(2) \end{gathered}`

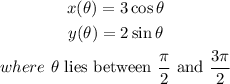
To find:

The graph of the parametric equations

When theta = pi/2, we'll have;

`\begin{gathered} x((\pi)/(2))=3\cos(\pi)/(2)=3*0=0 \\ y((\pi)/(2))=2\sin(\pi)/(2)=2*1=2 \end{gathered}`

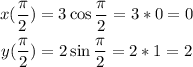
When theta = 3pi/4;

`\begin{gathered} x((3\pi)/(4))=3\cos(3\pi)/(4)=(-3√(2))/(2) \\ y((3\pi)/(4))=2\sin(3\pi)/(4)=√(2) \end{gathered}`

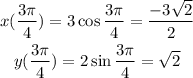
When theta = pi;

`\begin{gathered} x(\pi)=3\cos\pi=3*(-1)=-3 \\ y(\pi)=2\sin\pi=2*(0)=0 \end{gathered}`

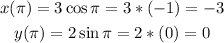
When theta = 5pi/4;

`\begin{gathered} x((5\pi)/(4))=3\cos(5\pi)/(4)=-(3√(2))/(2) \\ y((5\pi)/(4))=2\sin(5\pi)/(4)=-√(2) \end{gathered}`

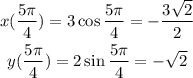
When theta = 3pi/2;

`\begin{gathered} x((3\pi)/(2))=3\cos(3\pi)/(2)=0 \\ y((3\pi)/(2))=2\sin(3\pi)/(2)=-2 \end{gathered}`

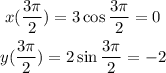
We can now go ahead and sketch the graph as seen below;