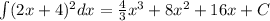1 Answer

Nikolay Tomitov · Answer 1 · 2023-10-05T23:03:08+0000

To solve this problem, we will use the following properties

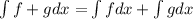
$\int f+gdx\text{ =}\int fdx+\int gdx$

(The integral of the sum is the sum of the integrals).

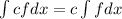
$\int cfdx=c\int fdx$

(The integral of a constant times a function is constant times the integral of the function)

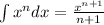
$\int x^ndx=(x^(n+1))/(n+1)^{}$

only when n is not -1.

First, recall that

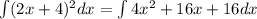
$\int (2x+4)^2dx=\int 4x^2+16x+16dx$

using the sum property, we have

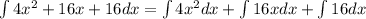
$\int 4x^2+16x+16dx=\int 4x^2dx+\int 16xdx+\int 16dx$

Now, we will solve each integral apart. We will use the last two properties to do so.

Note that

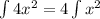
$\int 4x^2=4\int x^2$

we identify that in this case, the function is of the form x^n where n=2. Then, using the last property we get

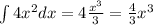
$\int 4x^2dx=4(x^3)/(3)=(4)/(3)x^3^{}$

Also, note that

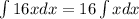
$\int 16xdx=16\int xdx$

we identify that the function is of the form x^n where n=1. Then,

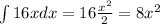
$\int 16xdx=16(x^2)/(2)=8x^2$

Finally, we have

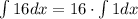
$\int 16dx=16\cdot\int 1dx$

we note that 1=x⁰. So we have

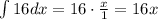
$\int 16dx=16\cdot(x)/(1)=16x$

Then, by adding all results we get

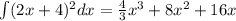
$\int (2x+4)^2dx=(4)/(3)x^3+8x^2+16x$

Since we are finding the function whose derivative is (2x+4)², we add a constant C. So we have

$\int (2x+4)^2dx=(4)/(3)x^3+8x^2+16x+C$

Your comment on this question: