Question

A truck covers 40.0 m in 7.10 s while uniformly slowing down to a final velocity of 1.25 m/s.(a) Find the truck's original speed. m/s(b) Find its acceleration. m/s2

Answer 1

original speed: 10 m/s

acceleration : -1.23 m(s^2) , or desaccelerating ar a t rate of 1.23 m/s^2

Step-by-step explanation

to solve this we need the formuilas

`\begin{gathered} v_f=v_0-at \\ \\ v_(f^2)=v^2_0-2ad \end{gathered}`

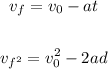
Step 1

Let

`\begin{gathered} \text{distance =d= 40 m} \\ \text{time}=\text{ t=7.1 s} \\ \text{ final velocity = v}_f=1.25\text{ }(m)/(s) \\ \text{acceleration}=a \\ v_o \end{gathered}`

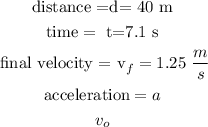
now, replace and solve for a

`\begin{gathered} v_f=v_0-at \\ 1.25\text{ }(m)/(s)=v_0-a(7.1\text{ s)} \\ 1.25=v_0-7.1a\rightarrow equation(1) \end{gathered}`

and,

`\begin{gathered} v^2_f=v^2_0-2ad \\ \text{replace} \\ 1.25^2=v^2_0-80a \\ 1.25^2=v^2_0-80a\rightarrow equation(2) \\ \end{gathered}`

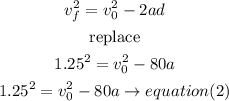
Step 2

solve the equations

`\begin{gathered} 1.25=v_0-7.1a\rightarrow equation(1) \\ 1.25^2=v^2_0-80a\rightarrow equation(2) \end{gathered}`

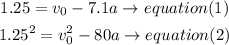
a) isolate the a value in equaion (1) and then replace in equation (2)

`\begin{gathered} 1.25=v_0-7.1a\rightarrow equation(1) \\ 1.25-v_0=-7.1a \\ (1.25-v_0)/(-7.1)=a \end{gathered}`

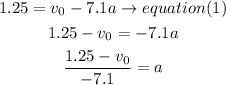
now,set equal in equation (2)

`\begin{gathered} 1.5625=v^2_0-80a\rightarrow equation(2) \\ 1.5625=v^2_0-80((1.25-v_0)/(-7.1)) \\ 1.5625=v^2_0+(100-80v_0)/(-7.1) \\ 1.5625=v^2_0+(100)/(7.1)-(80v_0)/(7.1) \\ 1.5625=v^2_0+14.08-11.26v_0 \\ 0=v^2_0+14.08+11.26v_0-1.5625 \\ 0=v^2_0+11.26v_0-12.5175 \\ v_0=10\text{ }(m)/(s) \end{gathered}`

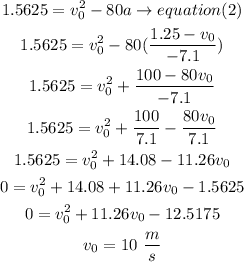
b) finally, replace the v0 value to find the acceleration

`\begin{gathered} (1.25-v_0)/(-7.1)=a \\ \text{replace} \\ (1.25-10)/(-7.1)=a \\ a=(-8.75)/(-7.1)=1.23\text{ }(m)/(s^2) \end{gathered}`

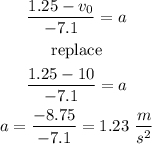
therefore,

original speed: 10 m/s

acceleration : -1.23 m(s^2) , or desaccelerating ar a t rate of 1.23 m/s^2