Question

Some bullfrogs were introduced into a small pond. The graph shows the bullfrog population for the next few years. Assume that the population grows exponentially.

equation: 140(315/140)^(t/2)
What is the growth rate?

Answer 1

For exponential growths,
population after time t = original population x (growth rate)^time
The growth rate works out to be:
(315/140)^(t/2)
= [√(315/140)]^t
= 1.5^t
The growth rate is 1.5 times per year.

Answer 2

50%

Explanation:

The general exponential growth function is,

`y(t)=a(1+r)^t`

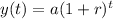
where,

y(t) is the function of time t, which represents the future amount,

a = initial amount,

r = growth rate in decimals,

The given function is,

`=140\left((315)/(140)\right)^{(t)/(2)}`

`=140\left((315)/(140)\right)^{(1)/(2)\cdot t}`

`=140\left(\left((315)/(140)\right)^{(1)/(2)\right)^t}`

`=140\left(\sqrt(315)/(140)\right)^t}`

`=140(1.50)^(t)`

`=140(1+0.50)^(t)`

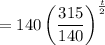
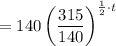
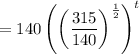
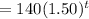
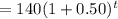
Comparing this with the general function, we get the growth rate as 0.50 or 50%