It is given that the triangles are similar, that is,
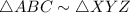
It is required to find the area of the larger triangle.
Recall that the scale factor, k of similar figures is the ratio of their corresponding sides:
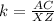
Substitute AC=5 and XZ=15 into the equation:
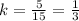
Hence, the scale factor is 1/3.
Recall that as per the Area of Similar Figures, the ratio of areas for two similar figures with a scale factor, k is:
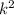
This implies that:
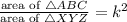
Substitute the values of the area of triangle ABC and the scale factor into the proportion:
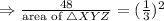
Let the area of ΔXYZ be A, and solve for A in the equation:
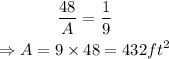
The required answer is 432 square ft.
The last choice is the answer.