Question

You deposit $4000 in an account earning 3% interest compounded monthly. How much will you have in the account in 15 years?

Answer 1

Given:

Principal, P = $4000

Interest rate, r = 3% = 0.03

Time, t = 15 years.

Number of times comounded, n = monthly = 12 months a year

Let's find the final Amount in the account after 15 years.

Apply the compound interest formula

`A=P(1+(r)/(n))^(nt)`

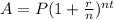
Where:

A is the final amount.

P = $4000

r = 0.03

t = 15

n = 12

Thus, we have:

`\begin{gathered} A=4000(1+(0.03)/(12))^(12*15) \\ \\ A=4000(0.0025)^(180) \\ \\ A=4000(1.0025)^(180) \\ \\ A=4000(1.567431725) \end{gathered}`

Solving further:

`A=6269.73`

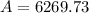
Therefore, the amount in the account in 15 years will be $6269.73

ANSWER:

$6269.73