Question

The endpoints of thedirected line segment ABare A (1,7) and B(5, 15).Find the coordinates of pointP along AB so that the ratioof AP to PB is 3 to 1.

Answer 1

The endpoints of a line segment AB are given as A(1,7) and B(5,15).

It is required to find the coordinates of a point P along AB so that the ratio of AP to PB is 3 to 1.

To do this, use the Internal Section Formula for a point P dividing the line segment AB with endpoints A(x1,y1) and B(x2,y2) in the ratio m:n.

The formula is given as:

`P(x,y)=\left((mx_1+nx_2)/(m+n),(my_1+ny_2)/(m+n)\right)`

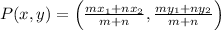
Substitute A(x1,y1)=(1,7), B(x2,y2)=(5,15) and m:n=3:1 into the formula:

`\begin{gathered} P(x,y)=\left((3(1)+1(5))/(3+1),(3(7)+1(15))/(3+1)\right)=\left((3+5)/(3+1),(21+15)/(3+1)\right) \\ =\left((8)/(4),(36)/(4)\right)=\left(2,9\right) \end{gathered}`

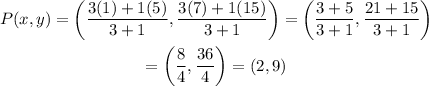
Hence, the required point is P(2,9).

The answer is P(2,9).