Question

Verify trigonometric equation by substituting identifies to match the right hand side of the equation to the left hand side of the equation. Show all work. Problem:-tan^2x + sec^2x=1

Answer 1

This identities are known as Pythagorean identities because this can be represented and solved using the pythagoras theorem. Let's remind the theorem:

`A^2+B^2=C^2`

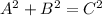
Now, we also should know that the trigonometric functions can be written using the sides of a triangle. For the tangent and secant, we know:

`\begin{gathered} \tan x=(B)/(A) \\ \sec x=(C)/(A) \end{gathered}`

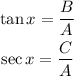
In the next step I will substitute this identities to the given equation:

`\begin{gathered} -\tan ^2x+\sec ^2x=1 \\ -((B)/(A))^2+((C)/(A))^2=1 \\ -(B^2)/(A^2)+(C^2)/(A^2)=1 \\ (C^2-B^2)/(A^2)=1 \\ C^2-B^2=A^2 \\ C^2=A^2+B^2 \end{gathered}`

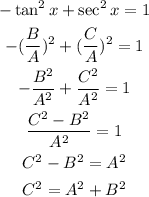
Which satisfy the Pythagoras Theorem.