Question

Find the first and second derivatives of f(x) 1-2x O f'(x) 2x-3 ex 5 - 2x f"(x) = O 3-2 f'(x) = 2x-5 F"(x) ex O f'(x) = 4xe* - 2e f"(x) = 4xe* + 2e O f'(x) = 2xe* - 3e* f'(x) = 2xe - ex

Answer 1

Given the function

`f\mleft(x\mright)=(1-2x)/(e^x)^{}`

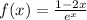
To compute the first derivative, we must recall the derivative of a quotient rule:

`((h)/(g))^(\prime)=(h^(\prime)g-g^(\prime)h)/(g^2)`

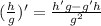
Here: h(x)=1-2x, g(x)=e^x

h'(x)=-2

g'(x)=e^x

substituting into the formula:

`f^(\prime)(x)=\frac{(-2)e^x-e^x(1-2x)^{}}{e^(2x)}^{}=(-2e^x-e^x+2xe^x)/(e^(2x))`

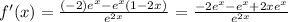
Operating:

`f^(\prime)(x)=(-3e^x+2xe^x)/(e^(2x))=e^x((-3+2x)/(e^(2x)))`

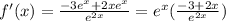
Simplifying numerator and denominator:

`f^(\prime)(x)=(-3+2x)/(e^x)`

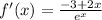
Looks like this matches the first choice

Now find the second derivative

This time: h(x)=-3+2x, h'(x)=2

g(x)=e^x, g'(x)=e^x

Applying the quotient rule again:

`f^(\prime)^(\prime)(x)=(2e^x-e^x(-3+2x))/(e^(2x))=(2e^x+3e^x-2xe^x)/(e^(2x))=(5e^x-2xe^x)/(e^(2x))`

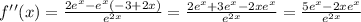
Factoring and simplifying:

`f^(\doubleprime)(x)=e^x\cdot(5-2x)/(e^(2x))=(5-2x)/(e^x)`

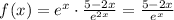
Both answers confirm the first choice is correct