Question

A spinner has 15 equal-size number sections. Enter the probability that the number you spin is a multiple of 5 or multiple of 3.

Answer 1

We have that probability is the number of successes of an event under the number or possible cases.

We have a spinner with 15 equal-size number sections. Therefore, there are the following possibilities:

1, 2, 3 ,4, 5 ,6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

The multiples of 3 (in this list of numbers) are:

3 * 1 = 3

3 * 2 = 6

3 * 3 = 9

3 * 4 = 12

3 * 5 = 15

The multiples of 5 are:

5 * 1 = 5

5 * 2 = 10

5 * 3 = 15

Therefore, we have:

There are 5 cases in which they are multiples of 3. Then, we have:

`P(m3)=(5)/(15)=(1)/(3)\Rightarrow P(m3)=(1)/(3)`

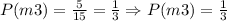
On the other hand, we have 3 cases in which they are multiples of 5. Thus:

`P(m5)=(3)/(5)`

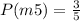
Therefore, the probability that the number you spin is a multiple of 5 or multiple of 3 is the sum of both probabilities:

`P_t=P(m3)+P(m5)=(1)/(3)+(3)/(5)=(5+9)/(15)\Rightarrow P_t=_{}(14)/(15)`

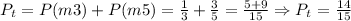
Therefore, the probability for this event is equal to 14/15.