We need to solve the next system of equations:
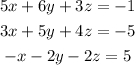
Lets pair equations to eliminate one variable:
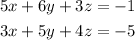
Multiply the first equation by -3 and the second equation by 5:
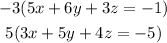
Then, add equations:
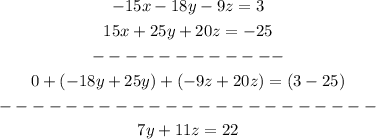
The second pair :
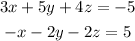
Multiply the first equation by 1 and the second equation by 3:
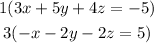
Add both equations:
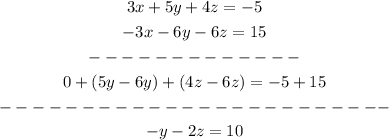
Solve the new system:
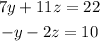
Multiply the first equation by 1 and the second equation by 7:
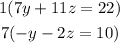
Add both equations:
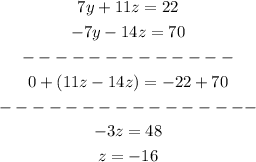
Replace the z value on one equation:
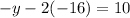
Solve for y:
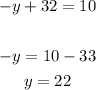
Finally, replace the y value and the z value:
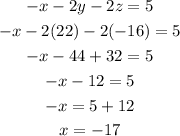
Hence, the result for the variables are:
x=-17
y=22
z=-16