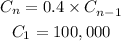Question

Fill in the tableWrite an explicit and recurisive equationHow many days will it take for the candy to be gone?

Answer 1

Since each day, the amount of candy that Augustus will give away is 60% of the actual amount of candy, the amount of candy that has on day n depends on the amount of candy remaining from the day n-1. Let C_n be the amount of candy remaining on day n.

Since 60% of the candy from the day n-1 will be given away, then only 40% from the candy of the day n-1 will remain on day n. Then:

`\begin{gathered} C_n=(40)/(100)* C_(n-1) \\ =0.4C_(n-1) \end{gathered}`

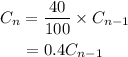
Since the amount of candy on day 1 is 100,000, then the recursive formula is:

`\begin{gathered} C_n=0.4C_(n-1) \\ C_1=100,000 \end{gathered}`

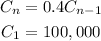
After n-1 days, the initial amount of candies gets multiplied by a factor of 0.4 n-1 times. Then, the explicit formula for the amount of candies that remain on day n (after n-1 days) is:

`\begin{gathered} C_n=(0.4)^(n-1)* C_1 \\ =0.4^(n-1)*100,000 \end{gathered}`

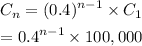
Therefore, the answers are:

Explicit formula:

`C_n=0.4^(n-1)*100,000`

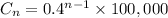
Recursive formula:

`\begin{gathered} C_n=0.4* C^{}_(n-1) \\ C_1=100,000 \end{gathered}`