Let t_0 be the half life of a radioactive element. Radioactive decay is modelled as a negative exponential function. Let A_0 be the initial amount of the sample. The amount A of radioactive element in that sample after t days is given by the formula:
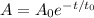
Substitute A_0=100kg, t=15.2 d and t_0=3.8d:
![\begin{gathered} A=(100\operatorname{kg})* e^(-15.2/3.8) \\ =(100\operatorname{kg})* e^(-4) \\ =(100\operatorname{kg})*0.0183156\ldots \\ =1.831563\ldots kg \end{gathered}]()
Therefore, the amount of radon-222 that is left from a 100kg sample after 15.2 days is, approximately:
![1.83\operatorname{kg}]()