We need to use the formula provided. The formula is:
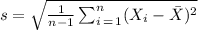
Where:
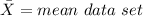
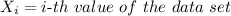
Then, first, we need to find the mean:
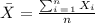
The data set is: 2, 3, 4, 4,7. Since there are 5 values, n = 5.
Now calculate:
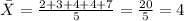
Now, we need to find the square of the difference between each value of the data set and the mean:
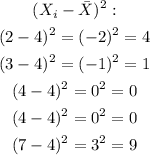
And now we need to find the sum of those numbers:
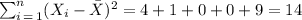
Now, we can calculate the standard deviation:
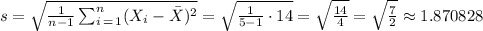
Thus, the correct answer is option a.) 1.87