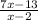Question

Show that 6 + [(x + 5) / ((x ^ 2 + 3x - 10)/(x - 1))] * s * i * m * p * l * i * f * i * e * s * t * o * (ax - b)/(cx - d) where a, b, c and d are integers.

Answer 1

The given expression is:

`6+\lbrack(x+5)/(x^2+3x-10)/(x-1)\rbrack`

Simplify the expression as follows:

Change the division sign to multiplication sign by swapping the denominator and numerator of the fraction on the right.

`6+\lbrack(x+5)*(x-1)/(x^2+3x-10)\rbrack`

Factorize the quadratic expression in the denominator:

`\begin{gathered} 6+\lbrack(x+5)*(x-1)/(x^2+3x-10)\rbrack_{} \\ \text{Rewrite 3x as 5x-2x, with the coefficients chosen such that their product is -10:} \\ =6+\lbrack(x+5)*(x-1)/(x^2+5x-2x-10)\rbrack_{} \\ =6+\lbrack(x+5)*(x-1)/(x(x+5)-2(x+5))\rbrack_{}=6+\lbrack(x+5)*(x-1)/((x+5)(x-2))\rbrack \end{gathered}`

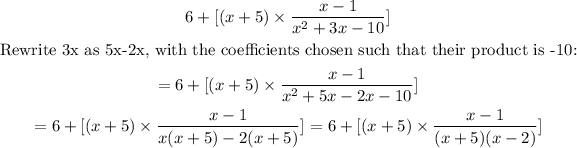
Cancel out common factors:

`\begin{gathered} 6+\lbrack\cancel{(x+5)}*\frac{x-1}{\cancel{(x+5)}(x-2)}\rbrack \\ =6+(x-1)/(x-2) \end{gathered}`

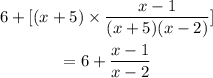
Simplify the expression:

`6+(x-1)/(x-2)=(6(x-2)+(x-1))/(x-2)=(6x-12+x-1)/(x-2)=(7x-13)/(x-2)`

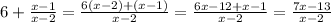
Hence, the expression has been simplified to the form (ax-b)/(cx-d), where a=7, b=13, c=1, and d=2.

The expression is simplified to:

`(7x-13)/(x-2)`