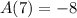Question

Let A(x) = integrate f(t) dt from 2 to x where f is the function given by the graph below .

Answer 1

We know that the function A(x) is defined as the integral:

`A(x)=\int_2^xf(t)dt`

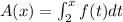
and that function f(t) is given in the graph.

a)

In this case we want to determine the value of A(3); according to the definition of the function A this will be given by:

`A(3)=\int_2^3f(t)dt`

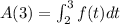
Now, geometrically this will mean that we would have to calculate the are under the curve of f(t) in the interval [2,3]; we show the area in the diagram below:

From it, we notice that this area is a triangle with base 1 and height 2; hence the area is:

`A_1=(1)/(2)(2)(1)=1`

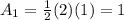
Therefore, we have that:

`A(3)=1`

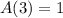
b)

Following the same procedure as before we have that:

`A(7)=\int_2^7f(t)dt`

The area we need to calculate in this case is shown below:

From the previous step we have the first one; areas 2 and 3 area the areas of a triangle and rectangle, respectively.

Triangle 2 has a vase of 2 and a height of 3 while rectangle 3 has a length of 2 and a width of 3, then we have:

`\begin{gathered} A_2=(1)/(2)(2)(3)=3 \\ A_3=(2)(3)=6 \end{gathered}`

Now, since areas 2 and 3 are below the x-axis this means that we that they are negative; with this in mind we have that the total area under the curve from 2 to 7 is:

`A=1-3-6=-8`

And therefore:

`A(7)=-8`