We have an investment that went from a initial value of PV = 1400 to a value of FV = 2177.36 in 71 months.
As the time is expressed in months, we assumed a monthly compounded interest, with a number of subperiods per year of m = 12.
Then, we have a total number of subperiods of n*m = 71.
We then can write the relation between the initial and final value as:
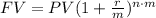
where r is the nominal rate.
We will calculate r as:
![\begin{gathered} (FV)/(PV)=(1+(r)/(m))^(n\cdot m) \\ \sqrt[n\cdot m]{(FV)/(PV)}=1+(r)/(m) \\ (r)/(m)=\sqrt[n\cdot m]{(FV)/(PV)}-1 \\ r=m\cdot(\sqrt[n\cdot m]{(FV)/(PV)}-1) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/oho6djz8uldc27yqdsnn.png)
Replacing with the values we get:
![\begin{gathered} r=m\cdot(\sqrt[n\cdot m]{(FV)/(PV)}-1) \\ r=12\cdot(\sqrt[71]{(2177.36)/(1400)}-1) \\ r\approx12\cdot(\sqrt[71]{1.555}-1) \\ r\approx12\cdot(1.00624-1) \\ r\approx12\cdot0.00624 \\ r\approx0.075 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rjldtaymn3lbn1d8ppt5.png)
We can now transformed this rate to an equivalent annually compounded rate as:
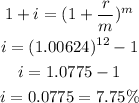
Answer: The equivalente annually compounded rate is 7.75%