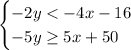
1. Solve the inequalities for y:
First ineqaulity: divide both sides of the inequality by -2 (as you divide by a negative number the inequality sing change to the opposite):
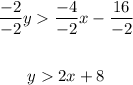
Second inequality: divide both sides of the inequality by -5:
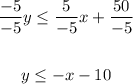
2. Define the kind of boundary line for each inequality:
When the inequality is < or > the boundary line is a dashed line.
When the inequality is ≥ or ≤ the boundary line is a solid line.
First inequality: as the inequality sing is > the boundary line is a dashed line.
Second inequality: as the inequality sing is ≤ the boundary line is a solid line.
3. Find two points (x,y) for each boundary line:
First inequality:
Line:
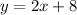
Find x when y is 0:
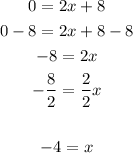
Point (-4,0)
Find y when x is 0:
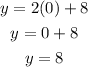
Point (0,8)
______________
Second inequality:
Line:
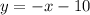
Find x when y is 0:
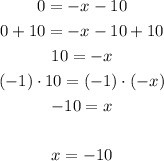
Point (-10,0)
Find y when x is 0:
![undefined]()