Question

Kuta Software - Infinite Algebra 2 Absolute Value Inequalities Solve each inequality and graph its solution. Periods Name Samantha cebaros Date 3/8/202 1) 6n1 = 18 2) Ip+4158 18 Long 방용 3nt3 blza --Lila -8LP+428 -BLHLPL-u -125psy 4) 15x1 5 10Question 14

Answer 1

To solve the exercise you can use this property of the absolute value:

`|x|\le a=-a\le x\le a`

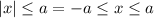
So, in this case, you have

`|6+9x|\le24=-24\le6+9x\le24`

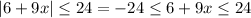
Then

`\begin{gathered} -24\le6+9x \\ \text{ and} \\ 6+9x\le24 \end{gathered}`

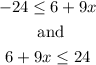
To solve the first part you can proceed like this:

`\begin{gathered} -24\le6+9x \\ \text{ Subtract 6 from both sides of the inequality} \\ -24-6\le6+9x-6 \\ -30\le9x \\ \text{ Divide by 9 from both sides of the inequality} \\ -(30)/(9)\le(9x)/(9) \\ -(30)/(9)\le x \\ \text{ Simplify} \\ -(3\cdot10)/(3\cdot3)\le x \\ -(10)/(3)\le x \end{gathered}`

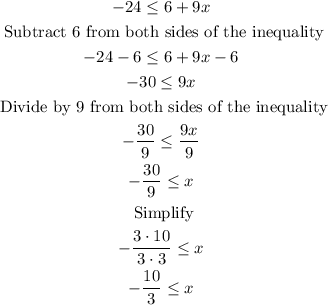
To solve the second part you can proceed like this:

`\begin{gathered} 6+9x\le24 \\ \text{ Subtract 6 from both sides of the inequality} \\ 6+9x-6\le24-6 \\ 9x\le18 \\ \text{ Divide by 9 from both sides of the inequality} \\ (9x)/(9)\le(18)/(9) \\ x\le2 \end{gathered}`

Therefore, the solution to the inequality will be

`-(10)/(3)\le x\le2`

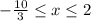
Graphically