We have this system of equations:
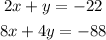
We can simplify the equations before starting as:
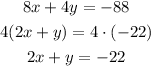
The two equations are the same, so we will have infinite solutions for this system.
If we applied the substitution method, we would have gotten the same result.
We would have multiplied the second equation by 1/4 and substract from the first equation:
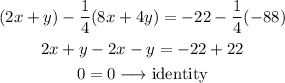
Any point lying in the line 2x+y=-22 is a solution to the system.
Answer: the system has infinite solutions as the equations are linear combinations of each other.