Equation for option 1.
Let x be the number of years since the aunt provides the money. In this case for each year x is pass you recieve the same amount, this means that this option can be represented by a linear equation. If y is the total amoun after x years then the money you have is:
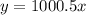
Equation for option 2.
Let x and y represent the same variables. In this case you begin with a dollar and each year the amount doubles; in this case the amount does not remain constant but follow the same pattern (it doubles each year) then the money amount at the end can be express as an exponential function:
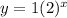
Therefore, the equation for option 1 is:
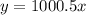
and for option 2 is:
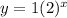
Now, to determine how much money each option will have when you turn 21 we plug x=17 in each equation. For option 1 you will have:
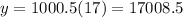
and for opyion 25 you will have:
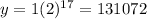
Therefore, option 2 is a better option since you will have $131,072 after 17 years; while in option 1 you will only have $17,008.50
This can be seen in the following graph:
The graph shows that after approximatelly 14 years option 2 returns more money.