Question

The radius of the Sun is 6.96 x 108 m and the distance between the Sun and the Earth is roughtly 1.50 x 1011 m. You may assume that the Sun is a perfect sphere and that the irradiance arriving on the Earth is the value for AMO, 1,350 W/m2. Calculate the temperature at the surface of the Sun.

Answer 1

5766.7 K

Step-by-step explanation:

We are given that

Radius of Sun , R=
`6.96* 10^(8) m`

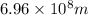
Distance between the Sun and the Earth, D=
`1.50* 10^(11)m`

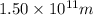
Irradiance arriving on the Earth is the value for AMO=
`1350W/m^2`

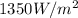
We have to find the temperature at the surface of the Sun.

We know that

Temperature ,T=
`((K_(sc)D^2)/(\sigma R^2))^{(1)/(4)}`

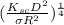
Where
`K_(sc)=1350 W/m^2`

`\sigma=5.67* 10^(-8)watt/m^2k^4`

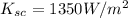
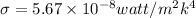
Using the formula

`T=((1350* (1.5* 10^(11))^2)/(5.67* 10^(-8)* (6.96* 10^(8))^2))^{(1)/(4)}`

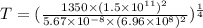
T=5766.7 K

Hence, the temperature at the surface of the sun=5766.7 K