Question

1. ** f(x) = -2x + 3. The function g(x) is perpendicular to f(x) and g(2) = 3. Which of the following equations could represent g(x)? (A) y = x-2 (B) y=-3x+4 (C) -x + 2y = 4 (D) 2x + 2y = 4

Answer 1

Answer:

-x + 2y = 4

Explanations:

The given function is:

f(x) = -2x + 3

The equation of a line is of the form:

y = mx + c

comparing this equation to f(x) = -2x + 3

m = -2

c = 3

When two lines are perpendicular to each other, the slope of one is the negative inverse of the other.

Since g(x) is perpendicular to f(x), it will have a slope, m = 1/2

Also, g(2) = 3

This means that, the line g(x) passes through the point (2, 3)

The point slope form of the equation of a line is:

y - y₁ = m(x - x₁)

Substituting m = 1/2 , x₁ = 2, and y₁ = 3 into the equation above:

`\begin{gathered} y\text{ - 3 = }(1)/(2)(x\text{ - 2)} \\ y\text{ -3 = }(1)/(2)x\text{ - }1 \\ y\text{ = }(1)/(2)x\text{ - 1 + 3} \end{gathered}`
`y\text{ = }(1)/(2)x\text{ + 2}`

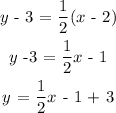
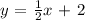
Multiply through by 2

2y = x + 4

-x + 2y = 4