Q2) We have to find the derivative of the function y = (ln x)^x.
We can start using the property of the derivative of an potential and exponential function:

In this case, u = ln(x) and v = x, so we can solve it as:
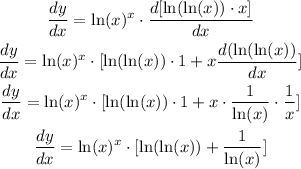
Answer: dy/dx = ln(x)^x * [ln(ln(x)) + 1/ln(x)]