Question

Find the exact value, without acalculator.30°sin 15°sintan 15° =2cos 15°30°COS2

Answer 1

The problem stated that

`\tan 15=(\sin 15)/(\cos 15)=(\sin(30)/(2))/(\cos(30)/(2))`

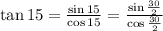
whereas sin 15 and cos 15 can be evaluated using half-angle formula. The half-angle formula for sine function is

`\sin (\theta)/(2)=\sqrt[]{(1-\cos \theta)/(2)}`

while the half-angle formula for cosine function is

`\cos (\theta)/(2)=\sqrt[]{(1+\cos \theta)/(2)}`

The theta value to evaluate the half-angle formula for tangent 15 is 30 degrees. We now proceed in calculating the value of the trigonometric function.

`\begin{gathered} \sin (30)/(2)=\sqrt[]{(1-\cos30)/(2)} \\ \cos (30)/(2)=\sqrt[]{(1+\cos30)/(2)} \end{gathered}`

The exact value of cosine 30 is √3/2, hence, the equation above now becomes

`\begin{gathered} \sin (30)/(2)=\sqrt[]{\frac{1-\frac{\sqrt[]{3}}{2}}{2}} \\ \cos (30)/(2)=\sqrt[]{\frac{1+\frac{\sqrt[]{3}}{2}}{2}} \end{gathered}`

Simplifying the equations above

`\begin{gathered} \sin (30)/(2)=\sqrt[]{\frac{\frac{2-\sqrt[]{3}}{2}}{2}}=\sqrt[]{\frac{2-\sqrt[]{3}}{4}} \\ \cos (30)/(2)=\sqrt[]{\frac{\frac{2+\sqrt[]{3}}{2}}{2}=}\sqrt[]{\frac{2+\sqrt[]{3}}{4}} \end{gathered}`

Since tangent theta is the ratio between the sin function and the cosine function, getting the ratio of the two equations above will result to

`(\sin(30)/(2))/(\cos(30)/(2))=\tan 15=\frac{\sqrt[]{\frac{2-\sqrt[]{3}}{4}}}{\sqrt[]{\frac{2+\sqrt[]{3}}{4}}}`

Simplifying,

`\begin{gathered} \tan 15=\sqrt[]{\frac{2-\sqrt[]{3}}{4}}\cdot\sqrt[]{\frac{4}{2+\sqrt[]{3}}} \\ \tan 15=\frac{\sqrt[]{2-\sqrt[]{3}}}{\sqrt[]{2+\sqrt[]{3}}}=\sqrt[]{\frac{2-\sqrt[]{3}}{2+\sqrt[]{3}}} \end{gathered}`

Where the equation above shows the exact value of tan 15.