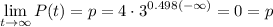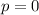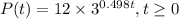
a. Find the number of fruit flies which were initially placed in the container.
Evaluate the function for t = 0

-----------------------------
b. Evaluate the function for t = 6
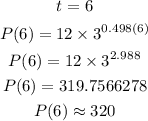
------------------------------------------------
c.
Evaluate the function for P(t) = 8000
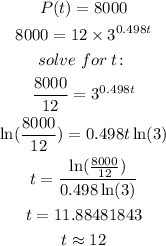
-----------------------------------
d.
Let's find the limit for t->-∞ :