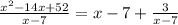To do a long division of polynomials, we will follow similar steps from the standard long division.
So, we start by putting the dividend and the divisor:
x - 7 | x² -14x +52
Now, we look for which polynomial we need to multiply the divisor so that we get a term that will be the same as the first term of the dividend, x². We can multiply the divisor by x, so we put x on the top and the result under the dividend to substract from it:
x
x - 7 | x² -14x +52
- x² -7x
-7x +52
Now, the new polynomial we have is -7x + 52, so we need a new polynomial to multiply our divisor so that we get the same as the first term, -7x. So, we can multiply the polynomial by -7, so we put the -7 on top and do the multiplication and the substraction:
x -7
x - 7 | x² -14x +52
- x² -7x
-7x +52
- -7x +49
3
Now that we obtained a polynomial (which is actually a constant) that has a degree less then aour divisor, we can't continue.
Now, to get the results, we look at the top part and the bottom part. The top part has x - 7, which means this is the quotient, and the bottom part has 3, which means this is the remainder.
So, the division (x² - 14x + 52) / (x - 7) has the quotient x - 7 and the remainder 3.
This means that we can answer this as: