Question

List each real zero of F according to the behavior of the graph at the X axis near that zero. If there’s more than one answer please separate with commas there is no answer put none.f(x)=-x^2(x+1)^2(x-1)Zero(s) where the graph crosses the x-axis:Zero(s) where the graph touches, but does not cross the x-axis:Find the y-intercept of the graph f:

Answer 1

The present problem presents the following equation:

`F(x)=x^2(x+1)^2(x-1)`

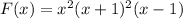
It follows the general form of a polynomial that which follows:

`F_{\text{general}}(x)=(x-a)^(na)(x-b)^(nb)(b-c)^(nc)\ldots`

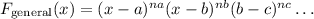
Where a, b, c... stands for the zeros of the function, and na, nb, nc... for its multiplicity.

According to the figure and the rule is given, the F presents three zeros:

`\begin{gathered} P1\colon(-1,0) \\ P2\colon(0,0) \\ P3\colon(1,0) \end{gathered}`

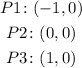
Analyzing each of them we are able to say that, P1 AND P2 have multiplicity equal to 2, and the graph touches but does not crosses the x-axis, while it crosses at P3.

The y-intercept is the point where x = 0, which implies P2.

From the solution presented above, we are able to answer the problem as follows:

Zero where the graph crosses the x-axis: x = 1

Zeros where the graph touches, buut does not cross the x-axes are: x = -1, 0

Thr y-intercept of the graph F is y = 0,0