SOLUTION
Newton's law of cooling states that the rate of change of temperature is proportional to the difference to the ambient temperature.
So, from here we have
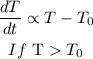
then the body should cool so the derivative should be negative, hence we insert the proportionality constant and arrive at
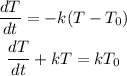
Can now use the integrating factor method of solving ODEs.
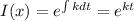
Multiplying both sides by I(x) we get

Notice that by using the product rule we can rewrite the LHS, leaving:
![(d)/(dt)[Te^(kt)]=e^(kt)kT_0](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/4ti9gdcr3vlvsfal57yw.png)
Integrate both sides with respect to t, we have
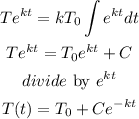
Average human body temperature is 98.6 degree fahrenheit, we have

we have
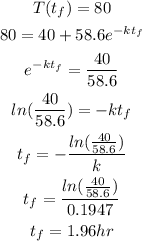
So from time of death, assuming body immediately started to cool, it took 1.96 hours to reach 80°F at which point it was found.
1.96 hr = 117,6 mins subtracting from 10 a.m, approximate time of death is 8 : 02 : 24 am
Hence the answer is
8 : 02 : 24 am