Question

Section 2.4 question: 5The table below shows the population of California from 2010 to 2019.YearPopulation (millions)201037.32011 37.6201238.0201338.3201438.6201538.9201639.2201739.4201839.5201939.5(a) Use a graphing calculator to build a logistic regression model that best fits this data, letting t=0 in 2010. Round each coefficient to two decimal places.Pt = (b) What does this model predict that the population of California will be in 2025? Round your answer to one decimal place. million people(c) When does this model predict that California's population will reach 40 million? Give your answer as a calendar year (ex: 2010).During the year (d) According to this model, what is the carrying capacity for California's population? million people

Answer 1

The graph for the logistic regression model is shown below

(a) From the graph, the model can be determined using the equation

`y_1\approx\frac{a}{1+e^{-b(x_1)_{}}}`

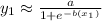
So from this equation,

`\begin{gathered} x_1\text{ represents t and } \\ y_1representsP_t \end{gathered}`

This becomes

`Pt_{}\approx\frac{a}{1+e^{-b(t_{})_{}}}`

Substituting the values of a and b into the equation above,

we have our logistic regression model as

`P_t=_{}\frac{74.91}{1+e^{-0.01(t_{})_{}}}`

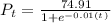
(b) Population of Carlifornia in 2025.

Here t = 15, because between 2010 to 2025 = 15 years.

From the model the population becomes

`\begin{gathered} P_t=_{}\frac{74.91}{1+e^{-0.01(t_{})_{}}} \\ P_(25)=_{}\frac{74.91}{1+e^{-0.01(15)_{}}} \\ P_(25)=(74.91)/(1+0.8607079) \\ P_(25)=(74.91)/(1.8607079) \\ P_(25)=40.258871 \\ P_(25)=40.3\text{ }millions\text{ to one decimal place } \end{gathered}`

Therefore, the answer is 40.3 millions

(c) When the population will reach 40 million?

From the analysis above, it will reach 40.3 million in 2025, 40.3 million is above 40 million, so let's check for 2023 and 2024, here t will be 13 and 14 respectively.

For 2023, we have

`\begin{gathered} P_(23)=_{}\frac{74.91}{1+e^{-0.01(13)_{}}} \\ P_(23)=39.886152 \\ P_(23)=39.9\text{ millions} \end{gathered}`

So in 2023, the population would be 39.9 millions

For 2024, we have

`\begin{gathered} P_(23)=_{}\frac{74.91}{1+e^{-0.01(14)_{}}} \\ P_(24)=_{}40.07252 \\ P_(24)=40.1\text{ m}illions\text{ } \end{gathered}`

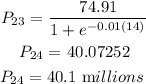
So in 2024, the population would be 40.1 millions which is very close to 40 millions as compared to 40.3 millions in 2025.

Hence the answer is 2024

(d) The Carrying Capacity of California population can be derived from the numerator value "a" of the logistic regression model.

Hence the answer is 74.91 million people