Question

Write an equation in standard form for the line that passes through (2, 4) and has slope 1/2. Which of the following equations best matches that standard form equation?a. x-2y=6 b. -x+2y=6c. -x+2y=3d. y = (1/2)x-3

Answer 1

So we have to find the equation of a line that passes through (2,4) and has a slope of 1/2 in standard form. First, we should write it in point-slope form because it will be easier to find it. Then we can change it into the standard form. The point-slope form of a line with a slope m that passes through point (a,b) is:

`y-b=m(x-a)`

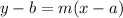
In this case we are told that the slope is 1/2 and the point is (2,4) so we get:

`y-4=(1)/(2)(x-2)`

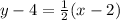
Now that we have the equation in point-slope form we must convert it into the standard form. This form looks like the following:

`Ax+By=C`

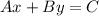
Where A, B and C are numbers. So let's take the equation we found before and distribute the product in the right side:

`\begin{gathered} y-4=(1)/(2)(x-2) \\ y-4=(x)/(2)-(2)/(2) \\ y-4=(x)/(2)-1 \end{gathered}`

Now let's add 4 to both sides:

`\begin{gathered} y-4=(x)/(2)-1 \\ y-4+4=(x)/(2)-1+4 \\ y=(x)/(2)+3 \end{gathered}`

We substract x/2 from both sides:

`\begin{gathered} y=(x)/(2)+3 \\ y-(x)/(2)=(x)/(2)+3-(x)/(2) \\ -(x)/(2)+y=3 \end{gathered}`

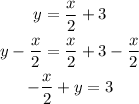
And finally we multiply both sides by 2:

`\begin{gathered} 2\cdot(-(x)/(2)+y)=2\cdot3 \\ -x+2y=6 \end{gathered}`

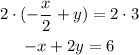
Then the answer is option b.