Question

(fully show the system of equations for each problem and the process used to solve the system.)Daphne has $4.50 in dimes and nickels. She has a total of 50 coins. How many of each kind does she have?

Answer 1

Given:

Let d represent the number of dimes coins.

Let n represent the number of nickels coins.

Recall:

`\begin{gathered} 1dime=10cents=\text{ \$0.10} \\ 1nickel=5cents=\text{ \$0.05} \end{gathered}`

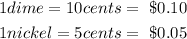
To generate the system of equations:

`\begin{gathered} She\text{ has a total of 50 coins:} \\ d+n=50..................................(1) \\ \\ \\ Total\text{ value of the 50 coins:} \\ 0.1d+0.05n=4.50.......................(2) \end{gathered}`

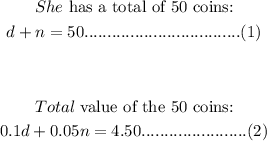
From equation (1);

`\begin{gathered} d+n=50 \\ d=50-n................................(3) \end{gathered}`

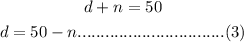
Substitute equation (3) into equation (2);

`\begin{gathered} 0.1d+0.05n=4.50 \\ 0.1(50-n)+0.05n=4.5 \\ 5-0.1n+0.05n=4.5 \\ 5-0.05n=4.5 \\ 5-4.5=0.05n \\ 0.5=0.05n \\ Divide\text{ both sides by 0.05 to get }n \\ (0.5)/(0.05)=n \\ n=10 \end{gathered}`

Substitute the value of n into equation (3);

`\begin{gathered} d=50-n \\ d=50-10 \\ d=40 \end{gathered}`

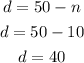
Therefore, Daphne has 40 dimes coins and 10 nickels coins.