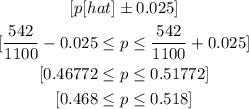Question

research institute poll asked respondents if they felt vulnerable to identify theft. n the poll n=1100 and x=542 who said yes use 90% confidence level identify the value of the margin of error E

Answer 1

The variable of interest is X: the number of people that answered positively when asked if they felt vulnerable to identity theft, out of 1100.

This variable has a binomial distribution.

To calculate a confidence interval for the population proportion of people that answered "yes" to the poll, you have to use the approximation to the standard normal distribution:

`Z=\frac{p\lbrack hat\rbrack-p}{\sqrt[]{(p\lbrack hat\rbrack(1-p\lbrack hat\rbrack))/(n)}}\approx N(0,1)`

The structure for the formula of the confidence interval is "estimator"±"margin of error"

Where the estimator is the sample proportion p[hat] and the margin of error has the following form:

`Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}\sqrt[]{(p\lbrack hat\rbrack(1-p\lbrack hat\rbrack))/(n)}`

To calculate the margin of error you have to determine the Z-value and the value of the sample proportion

Z-value, determine the probability, and then look for the value on the Z-table:

Confidence level: 1-α= 0.90

α=0.1

α/2=0.05

`Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}=Z_(\mleft\lbrace1-0.05\mright\rbrace)=Z_(\mleft\lbrace0.95\mright\rbrace)=1.645`

The sample proportion can be calculated by dividing the number of successes, in this case, the number of people that answered "yes" by the total number of people surveyed:

`\begin{gathered} p\lbrack hat\rbrack=(x)/(n) \\ p\lbrack hat\rbrack=(542)/(1100) \\ p\lbrack hat\rbrack=0.4927\approx0.493 \end{gathered}`

With these values you can determine the margin of error of the confidence interval as follows:

`\begin{gathered} Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}\sqrt[]{(p\lbrack hat\rbrack(1-p\lbrack hat\rbrack))/(n)} \\ 1.645\cdot\sqrt[]{((542)/(1100)(1-(542)/(1100)))/(1100)=0.0249\approx0.025} \end{gathered}`

The margin of error of the 90% confidence interval for the population proportion is 0.025

Confidence interval:

`\begin{gathered} \lbrack p\lbrack hat\rbrack\pm0.025\rbrack \\ \lbrack(542)/(1100)-0.025\leq p\leq(542)/(1100)+0.025\rbrack \\ \lbrack0.46772\leq p\leq0.51772\rbrack \\ \lbrack0.468\leq p\leq0.518\rbrack \end{gathered}`