Which are the solutions of x2 = –5x + 8?

Question

asked Jun 26, 2017 43.2k views

2 Answers

Ssayols · Answer 1 · 2017-06-30T07:27:53+0000

Answer:

x=1.53

x=6.53

Explanation:

The first thing to do is to leave the equation equal to zero expressed.

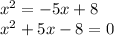
$x^(2) =-5x+8\\x^(2)+5x-8=0$

Next, being a second degree equation, we can use the general formula to find the solutions. This equation is as follows:

$x=\frac{-b+-\sqrt{b^(2)-4ac } }{2a}$

Where a is the coefficient of the quadratic term, b the coefficient of the linear term and c the coefficient of the value without variable.

In this case: a=1, b=5, c=-8

Replacing in the ecuation

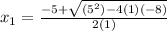
$x_(1) =\frac{-5+\sqrt{(5^(2))-4(1)(-8) } }{2(1)}$

x_(1) =(-5+√(25+32) )/(2)= (-5+√(57) )/(2) = (-5+7.54)/(2) =(2.54)/(2) =1.27

Now

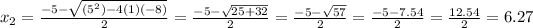
$x_(2) =\frac{-5-\sqrt{(5^(2))-4(1)(-8)} }{2}=(-5-√(25+32) )/(2)= (-5-√(57) )/(2) = (-5-7.54)/(2)  =(12.54)/(2) =6.27$

So, both solution:

x=1.53

x=6.53