Question

In the circle below, segment CB is a diameter. If the length of CDB is 14, what is the length of the radius of the circle?

Answer 1

GIVEN:

We are given a circle with center A and diameter CB.

The length of arc CDB is 14;

`arcCDB=14\pi`

Required;

We are required to calculate the lenght of the radius.

Step-by-step solution;

The length of an arc with the central angle measured in radians is;

`s=r\theta`

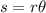
The length of the arc is given, so also is the angle theta (180 degrees, that is half the circle).

We can convert the degree measure of the angle into radians as follows;

`\begin{gathered} Degrees\Rightarrow Radians \\ (r)/(\pi)=(d)/(180) \end{gathered}`

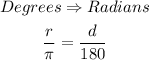
Now we substitute the value of d (degree measure);

`\begin{gathered} (r)/(\pi)=(180)/(180) \\ \\ (r)/(\pi)=1 \\ \\ Cross\text{ }multiply: \\ \\ r=\pi \end{gathered}`

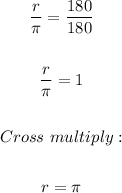
Now we take the formula for the length of an arc as follows;

`\begin{gathered} s=r\theta \\ Therefore: \\ \\ 14\pi=r\pi \end{gathered}`

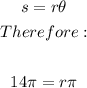
Divide both sides by pi;

`14=r`

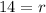
Therefore, the radius is

ANSWER:

`Radius=14\text{ }units`