Question

The length of a Ping-Pong table is 2 feet less than twice the width. The area of the Ping-Pong table is 40 square feet. What are the dimensions of the table?

Answer 1

width : 4 ft

length: 10 ft

Step-by-step explanation

Step 1

let L represents the length of the table

Let W represents the width of the table

if

The length of a Ping-Pong table is 2 feet less than twice the width.

`\begin{gathered} L=2\cdot\text{width -2} \\ L=2w-2\text{ Equation(1)} \end{gathered}`

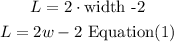
and the area of the Ping-Pong table is 40 square feet

`\begin{gathered} A=width\cdot length \\ A=40ft^2 \\ so \\ \text{width}\cdot\text{length}=40ft^2 \\ w\cdot L=40\text{ Equation(2)} \end{gathered}`

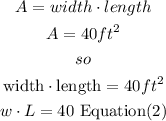
Step 2

solve the system of equations

`\begin{gathered} L=2w-2\text{ Equation(1)} \\ w\cdot L=40\text{ Equation(2)} \end{gathered}`

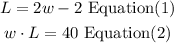
a)replace equation(1) in equation (2)

`\begin{gathered} w\cdot L=40\text{ Equation(2)} \\ w\cdot(2w-2)=40\text{ } \\ 2w^2-2w=40 \\ \text{subtract 40 in both sides} \\ 2w^2-2w-40=40-40 \\ 2w^2-2w-40=0\text{ }\Rightarrow ax^2+bx+c=0 \\ \text{Hence, use the quadratic formula to find w} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ w=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(2)(-40)}}{2\cdot2} \\ w=\frac{2\pm\sqrt[]{4+320}}{4} \\ w=(-2\pm18)/(4) \\ we\text{ just take the positive number, so} \\ w=(-2+18)/(4)=(16)/(4)=4 \end{gathered}`

therefore, the width is 4 ft

Step 3

finally,replace the valuw of w in equation (2) to find L

`\begin{gathered} w\cdot l=40 \\ L=(40)/(w) \\ L=(40)/(4) \\ L=10\text{ ft} \\ \end{gathered}`

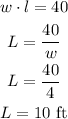
so, the length is 10 ft