Question

A theater group made appearances in two cities. The hotel charge before tax in the second city was $1500 higher than in the first. The tax in the first city was%, and the tax in the second city was 4%. The total hotel tax paid for the two cities was $665. How much was the hotel charge in each city before tax?

Answer 1

Let x be the charge before taxes of the first city and y the charge before taxes of the second city. We will translate each of the given facts about this two quantities into equations that will help us to find the values of x and y.

The first given fact is "The hotel charge before tax in the second city was 1500 higher than in the first one". This means that if we add 1500 to the charge of the first city, we would get the second city's charge. This leads to the equation

`y=x+1500`

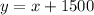
We are given the tax rate of each city and that the total amount paid of hotel tax was 665. This means that if we calculate the tax amount for each city and then add this quantities, we should get 665.

Since the tax rate of the first city is 7% (or 7/100) we can calculate the tax of the first city by multiplying x and 7/100. So the tax of the first city would be

`x\cdot(7)/(100)`

as the tax rate of the second city is 4%, following the same procedure we have that the tax amount of the second city is

`y\cdot(4)/(100)`

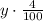
Then, adding this amounts together, we get

`x\cdot(7)/(100)+y\cdot(4)/(100)=665`

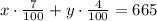
If we multiply each side by 100, we get

`7x+4y=66500`

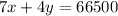
Using the first equation to replace the value of y in terms of x, we get

`7x+4\cdot(x+1500)=66500`

If we operate on the left side, we get

`7x+4\cdot(x+1500)=7x+4x+6000=11x+6000`

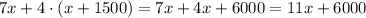
So we have the equation

`11x+6000=66500`

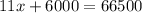
Now, we subtract 6000 from both sides, so we get

`11x=66500\text{ -6000=60500}`

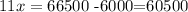
Finally, we divide by 11 on both sides, so we get

`x=(60500)/(11)=5500`

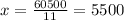
Now, we replace this value in the first equation, so we have

`y=x+1500=5500+1500=7000`

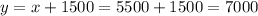
So the charge before tax in the first city was 5500 and 7000 in the second one.