6) It has one solution 7) infinite solution
Step-by-step explanation:
3/4 (x-1) - 1/2 = 2(1-3x)
By expanding:
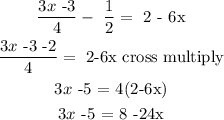
By collecting like terms:
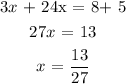
To determine what category it belongs, we need to understand our variable (x) is equal to a value (13/27). When this happens, we say it has one solution.
7) 2x + 4 = x + x + 3+1
2x + 4 = 2x +4
2x-2x = 4-4
0 = 0
When we have the right side of the equation equal to the left side, then it has infinite number of solution.