Question

Atmospheric pressure decreases by about 12% for every kilometer you climb. The pressure at sea levelis about 1013 atmospheres.20. Construct a model to represent the atmospheric pressure at a given altitude in kilometers.21. How many atmospheres of pressure will you feel at 5.895 km? (Top of Mt. Kilimanjaro) (round to the nearestatmosphere)22. How many atmospheres of pressure will you feel at 8.848 km? (Top of Mt. Everest) (round to the nearestatmosphere)23. How many atmospheres of pressure will you feel at 0.383 km? (highest point in Indiana) (round to the nearestatmosphere)

Answer 1

20) We have to model the variation of the atmospheric pressure with the height.

We know that it is 1013 atm at sea level and it decreases by 12% for every kilometer climbed.

Then, we can consider the sea level to be h = 0.

We then will have a pressure P(0) = 1013.

We can also relate the pressures with one kilometer of difference as:

`\begin{gathered} P(h+1)=P(h)-0.12P(h) \\ P(h+1)=(1-0.12)\cdot P(h) \\ P(h+1)=0.88\cdot P(h) \\ (P(h+1))/(P(h))=0.88 \end{gathered}`

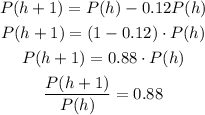
We can model this type of relations with an exponential model:

`P(h)=A\cdot b^h`

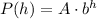
We then have to find the values of parameters A and b.

We then start with A, that will correspond to the initial value of P, as:

`P(0)=A\cdot b^0=A=1013`

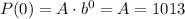
Then, we can calculate b as:

`\begin{gathered} (P(h+1))/(P(h))=0.88 \\ (A\cdot b^(h+1))/(A\cdot b^h)=0.88 \\ b^(h+1-h)=0.88 \\ b^1=0.88 \end{gathered}`

Then, b = 0.88 and we can write the model as:

`P(h)=1013\cdot0.88^h`

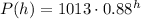
21) We can calculate the pressure when h = 5.895 km using the model as:

`\begin{gathered} P(5.895)=1013\cdot0.88^(5.895) \\ P(5.895)\approx1013\cdot0.4707 \\ P(5.895)\approx477 \end{gathered}`

22) We now have to calculate the pressure for the top of the Mt. Everest (h = 8.848 km):

`\begin{gathered} P(8.848)=1013\cdot0.88^(8.848) \\ P(8.848)\approx1013\cdot0.3227 \\ P(8.848)\approx327 \end{gathered}`

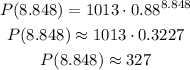
23) We finally have to calcualte the pressure for h = 0.383:

`\begin{gathered} P(0.383)=1013\cdot0.88^(0.383) \\ P(0.383)\approx1013\cdot0.9522 \\ P(0.383)\approx965 \end{gathered}`

Answer:

20) The model is P(h) = 1013*0.88