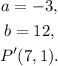Question

Point P(4,-2) undergoes a translation given by (x,y) - (x+3, x-a) followed by another translation (x,y) - (x-b, x+7) to produce the image of P” (-5,8). find the values of a and b and point P’.

Answer 1

• In this problem, we are moving from point P, to point P', and then to point P''.

,

• To move from one point to another, we make translations of the points.

,

• The ticks of the points are simply a notation. One tick denotes the point where you are after the first translation. Two ticks denote the point where you are after the second translation.

• Mathematically, a translation from a point P to a new point P' consists in summing numbers to the coordinates of the point P to get the coordinates of the new point P'.

,

• For example, if we have the point P with coordinates (x,y), and we move that point 3 units to the right, and 4 units up, we get the point P' with coordinates:

`P^(\prime)=(x+3,y+4)\text{.}`

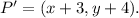
This problem consists of the following:

1) We start with a point P(4,-2) with coordinates x = 4 and y = -2.

2) We make the first translation, which consists in going from point P to point P'.

The coordinates of point P' are given by:

`P^(\prime)=(x+3,y-a).`

The coordinates x and y in that formula are the values of x and y of the original point. So we must replace x = 4 and y = -2 in the formula above. Doing that we have the following coordinates for the point P':

`P^(\prime)=(4+3,-2-a)=(7,-2-a)\text{.}`

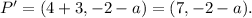
3) We made the first translation. Now we will do another translation, from point P' with coordinates x = 7 and y = -2 - a, to the point P'' with coordinates:

`P^(\prime\prime)=(x-b,y+7).`

Replacing the values x = 7 and y = -2 - a we get the following coordinates for P'':

`\begin{gathered} P^(\prime\prime)=(7-b,-2-a+7), \\ P^(\prime\prime)=(7-b,5-a), \end{gathered}`

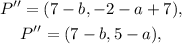
4) Finally, doing the translations we get the following coordinates for point P'':

`P^(\prime\prime)=(7-b,5-a)\text{.}`

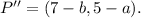
But from the statement of the problem, we know that the coordinates of point P'' are:

`P^(\prime\prime)=(-5,8)\text{.}`

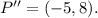
Comparing each coordinate we have the following equations:

`7-b=-5,\text{ and }^{}5-a=8.`

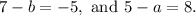
Solving the equation of b, we get:

`\begin{gathered} 7-b=-5, \\ 7=-5+b, \\ b=7+5, \\ b=12. \end{gathered}`

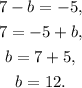
Solving the equation of a, we get:

`\begin{gathered} 5-a=8, \\ 5=8+a, \\ a=5-8, \\ a=-3. \end{gathered}`

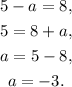
So the values of a and b are:

`\begin{gathered} a=-3, \\ b=12. \end{gathered}`

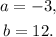
5) Using the value a = -3, the coordinates of point P' are:

`P^(\prime)=(7,-2-(-3))=(7,-2+3)=(7,1)\text{.}`

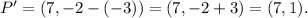
Answers

`\begin{gathered} a=-3, \\ b=12, \\ P^(\prime)(7,1)\text{.} \end{gathered}`