Question

Form a polynomial whose zeros and degree are given. 12) Zeros: 2, multiplicity 2; -2, multiplicity 2; degree 4 F) f(x) = x4 - 4x3 + 8x2 - 8x + 16 H) f(x) = x4 - 8x2 + 16 G) f(x) = x4 + 8x2 + 16 J) f(x) = x4 + 4x3 - 8x2 + 8x - 16

Answer 1

To answer this question we have to rememeber that a polynomial, in principle, will have the same number of zeros as the degree of the polynomial. When a polynomial has less than zeros that its degree we said that a soluton has multiplicity.

In this case we are looking for a polynomial of degree 4 that has two zeros, one in the point x=2 and the other in the point x=-2; both of them have to have multiplicity 2; that is, they appear twice in the solution.

To find the polynomial that we are looking for we are going to try and factor the polynomials given, so that we can see their behavior. Once we do that we are going to graph the one we think is the answer to confirmed thet we are right.

Fist option:

`f(x)=x^4-4x^3+8x^2-8x+16`

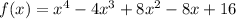
Let's factor this polynomial

`x^4-4x^3+8x^2-8x+16=x^3(x-4)+8(x^2-x+2)`

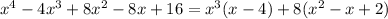
We can't factor more this polynomial, so we can't know its zeros by normal means. Let's graph the function:

From the graph we see that this function doesn't have zeros in the real numbers. (As we knew already from the factorization).

Second option.

`f(x)=x^4+8x^2+16`

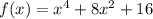
This function can be factor as

`\begin{gathered} x^4+8x^2+16=(x^2+4)(x^2+4) \\ =(x^2+4)^2 \end{gathered}`

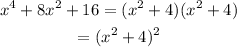
From the last expression we can readily find its zeros, we just have to equate this to zero and find x, doing so we have

`\begin{gathered} (x^2+4)^2=0 \\ x^2+4=0 \\ x^2=-4 \\ x=\pm\sqrt[]{-4} \\ x=\pm2i \end{gathered}`

From this, we can conlude that this function has two solutions of multiplicity 2, but this solutions ARE NOT REAL ONES. Therefore this is not the function we are looking for.

Third option.

`f(x)=x^4-8x^2+16`

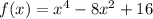
Let's factor this polynomial.

`\begin{gathered} x^4-8x^2+16=(x^2-4)(x^2-4) \\ =(x^2-4)^2 \end{gathered}`

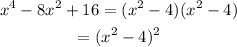
To find the zeros we hust equate to zero and solve for x

`\begin{gathered} (x^2-4)^2=0 \\ x^2-4=0 \\ x^2=4 \\ x=\pm\sqrt[]{4} \\ x=\pm2 \end{gathered}`

From this we see that the zeros of this function are x=2 and x=-2; and that each of this has multiplicity 2. Therefore this function fulfill everything we are looking for.

We can also see this from the graph of the function.

Fourth option.

`f(x)=x^4+4x^3-8x^2+8x-16`

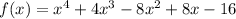
This function can't be factor in the real numbers (much like the first one) but let's take a look at its graph to see the zeros.

We notice tha the function has real zeros but they are not in the points we like.

Therefore, the function we are looking for is in option H.

That's it. Do you have any questions?

No problem.