Question

Solve the system of linear equations by substitution. Enter your answer as an ordered pair.

Answer 1

Write out the equation given

`\begin{gathered} y=-4x+40\ldots\text{equation 1} \\ y=x-15\ldots\text{equation 2} \end{gathered}`

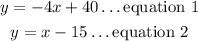
From equation 2, substitute the expression for y into equation 1

Then

`\begin{gathered} y=-4x+40 \\ \text{ Sunce y=x-15 in equation 2} \\ \text{Then we substitute into equation 1, to obtain} \\ x-15=-4x+40 \end{gathered}`

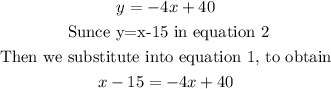
Isolate like term on one side of the equation

`\begin{gathered} x-15=-4x+40 \\ x+4x=40+15 \\ 5x=55 \end{gathered}`

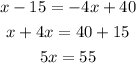
Divide both sides by 5, we have

`\begin{gathered} (5x)/(5)=(55)/(5) \\ \text{Then} \\ x=11 \end{gathered}`

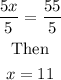
Substitute the value of x into equation 1 to fnd y, we have

`\begin{gathered} \text{equation 1 is } \\ y=x-15 \\ \text{ Recall x=11} \\ y=11-15 \\ \text{Then} \\ y=-4 \end{gathered}`

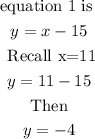
Therefore

Answer: X = 11, y = - 4